来自 CMU & 微软
没有说明是否在线上有应用

背景

”最小搜索次数“的分布很不均匀，
IVF下，80%的请求只需要检索小于等于 6/7/12 个倒排链；但长尾的20%需要最多 606/367/169 个倒排链 （DEEP/SIFT/GIST）
HNSW下：80%的请求需要小于等于 547/481/1260次距离计算（在layer0 扫过这么多点）；但长尾的20%却需要 88696/16618/118277（DEEP/SIFT/GIST）


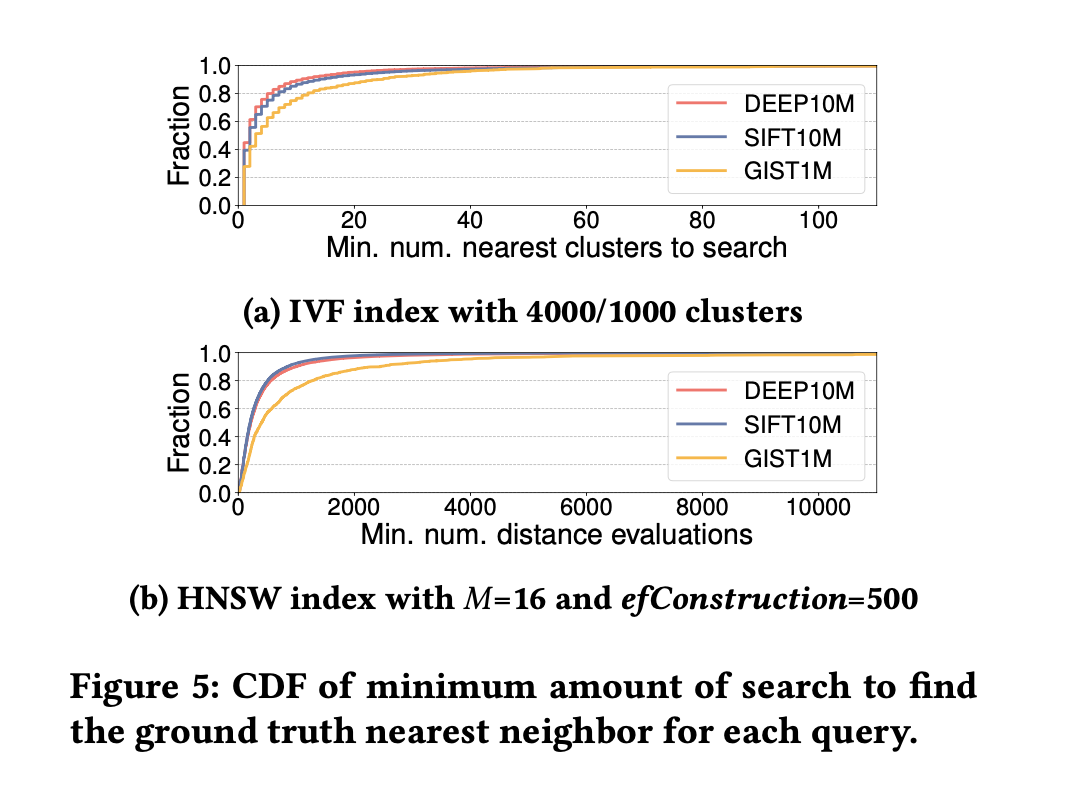
PS：此处的“最小搜索次数”是根据 Recall-@1 来定义的：在检索到groudtruth 的 top1 点的时候，扫过了多少cluster / 多少次距离计算。

核心思路

只建模静态query的特征是不够准确的（论文没有具体探究原因，但也可以大概猜到：除了query的特征，“最小搜索次数”和数据分布/索引内部结构也是非常相关的）。
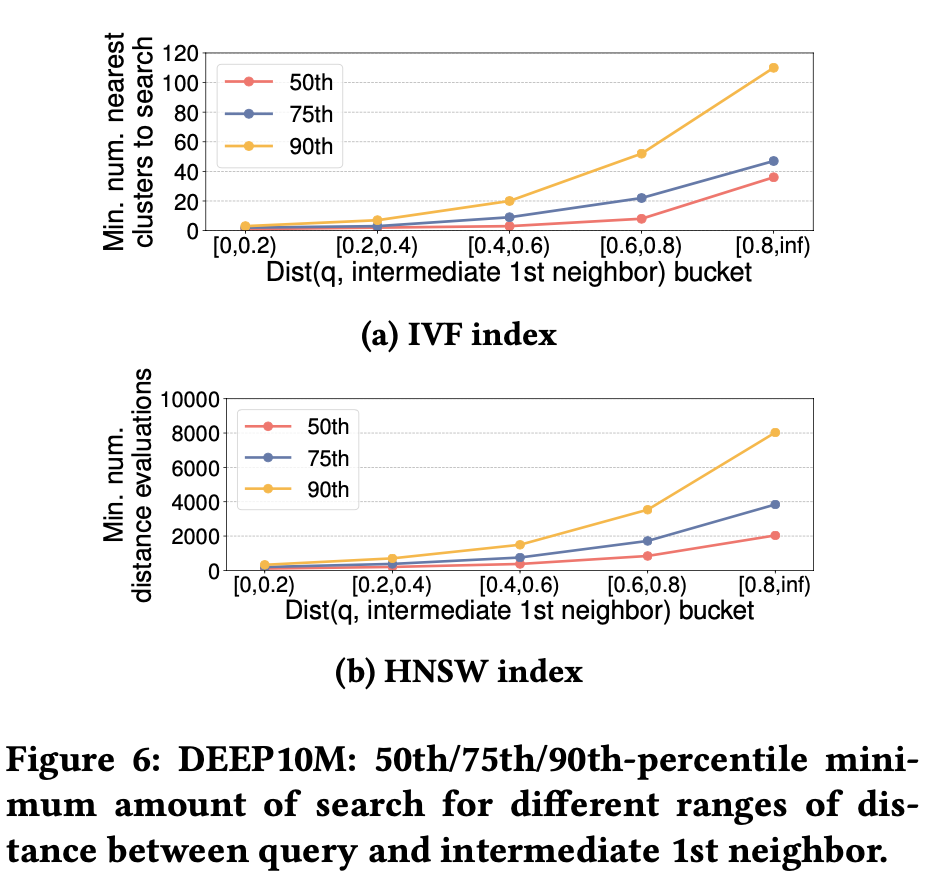
论文中增加了另外一种“动态”特征进行建模：中间结果top1与query的距离。
实验可以看到，中间结果top1与query距离越大，是越有可能有更大的“最小搜索次数”的。直观的解释：“if your search result is still far away from the query, you probably want to search more”。



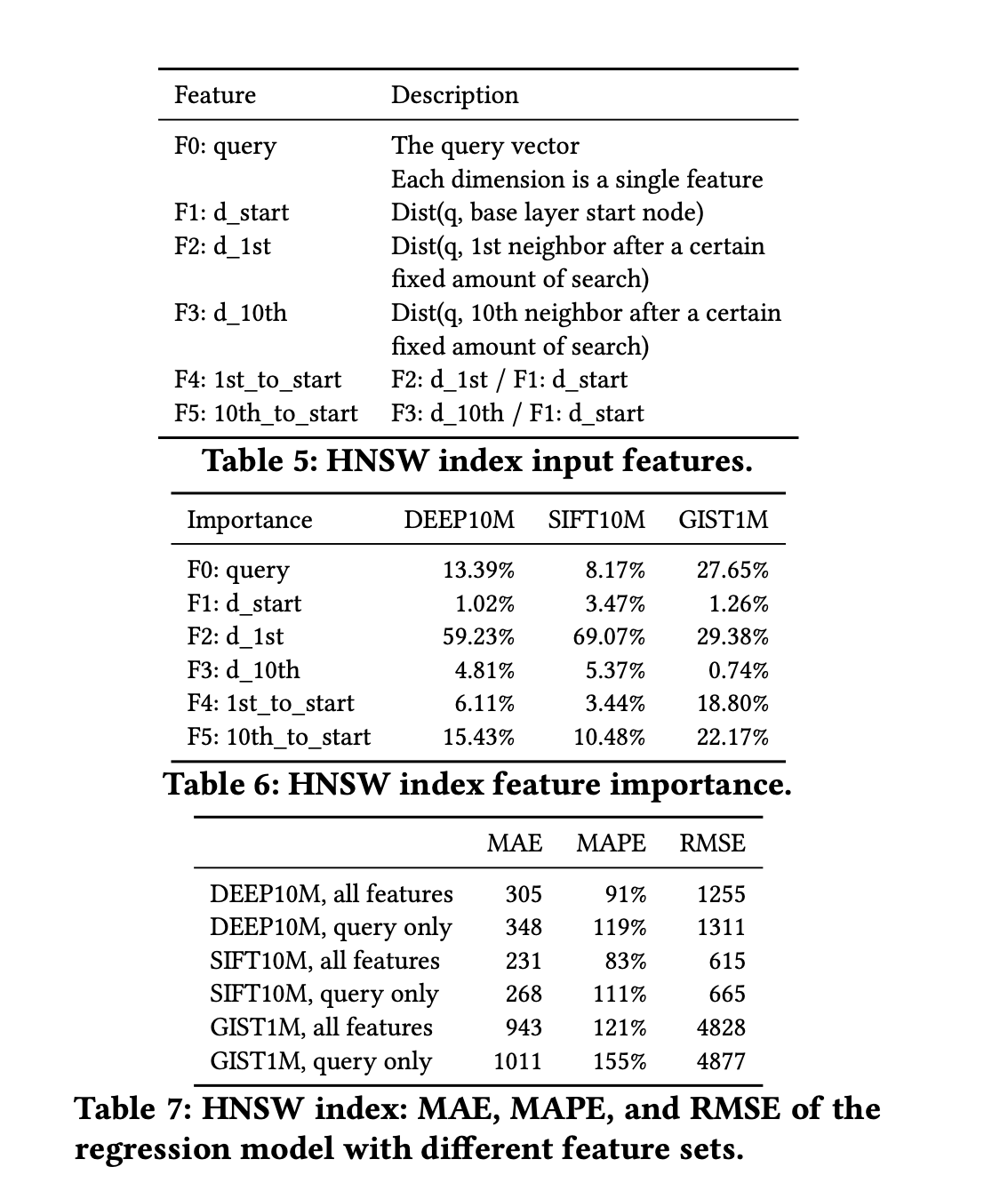
具体的模型使用的是梯度提升决策树（GBDT）。
原因：快速且效果不错

输入是：上图中五种特征
输出：预测的“最小搜索次数”

实现

以HNSW为例，在base layer之上仍然进行不加限制的beam search。
到了base layer，首先进行一个固定搜索次数的beam search。
到达固定的搜索次数后，进行一次终止条件预测，得到终止搜索次数p
a. 如果当前的搜索次数大于等于p，则认为已经找到结果
b. 如果当前搜索次数小于p，则继续beam search，知道达到p

效果

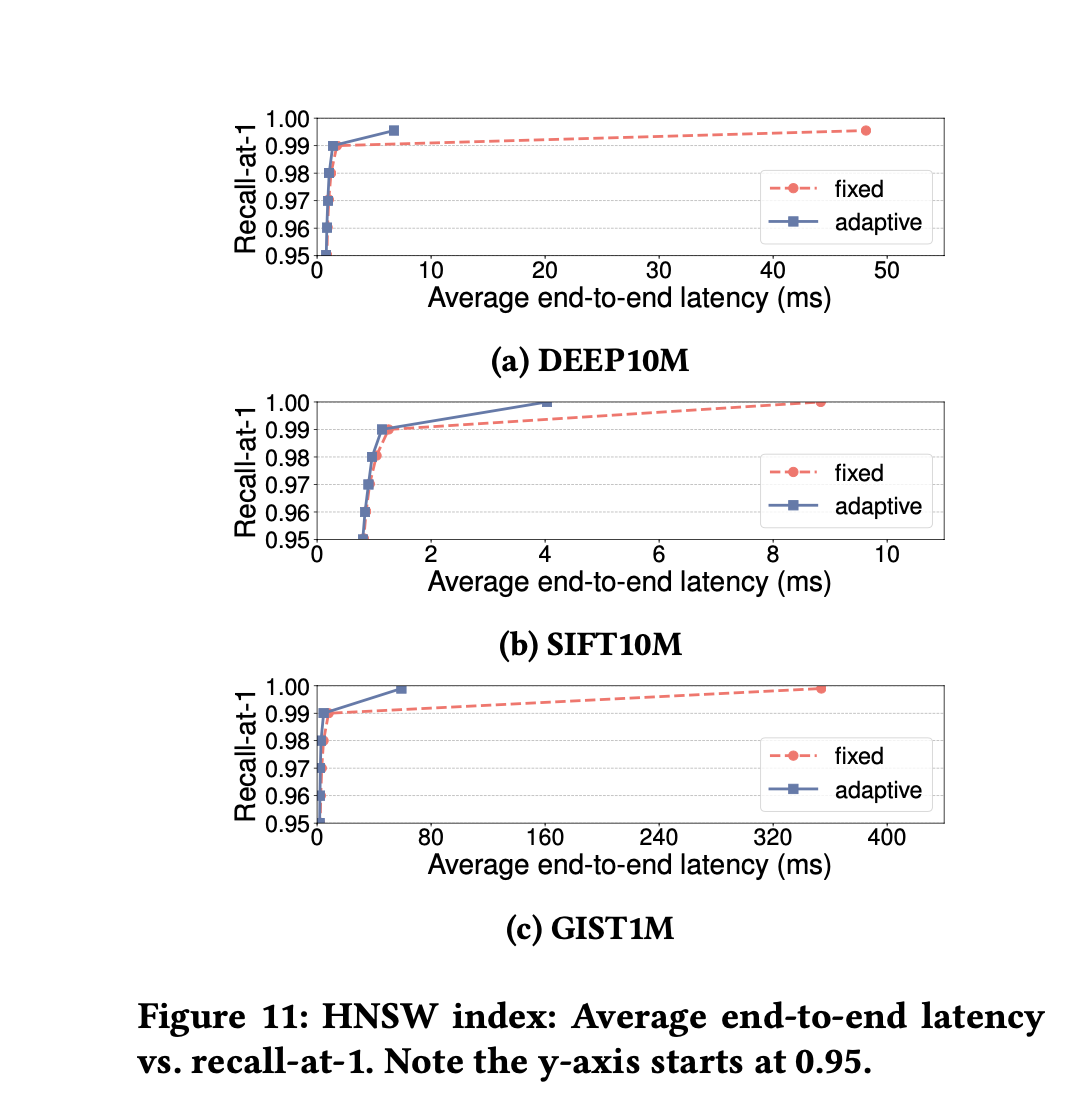
对长尾检索改善明显，2%~86%的提升

问题

• 模型建立的基础数据是检索到top1的“最小搜索次数”，放大到topk，效果是否还ok是存疑的
  • 对于IVF来说，这个问题可能不是很严重，但对于HNSW来说，原先的终止条件变成了
• 初始时的搜索次数（f）如何确定？
  • 论文是使用的固定的数据集，提前通过query及其groudtruth的对比拿到了这些数据。
  • 而且这个f值的确定和query分布有很大关系

资料

GBDT 梯度提升决策树
https://www.cnblogs.com/techflow/p/13445042.html